第一节 一个主宰性的比率
把一条线段分割为两部分,使其中一部分与全长之比等于另一部分与这部分之比,其比值是一个无理数,用分数表示为(√5-1)/2,取其前三位数字的近似值是0.618。由于按此比例设计的造型十分美丽,因此其被称为黄金分割率或者菲波纳奇比率,当然由这个比率还可以推出其他的菲披纳奇衍生比率。这个数值的作用不仅仅体现在诸如绘画(主要是达·芬奇的名作蒙娜丽莎,请看图7-1)、雕塑、音乐、建筑等艺术领域,而且在管理、工程设计等方丽也有若不可忽视的作用。自然界中更是随处可以看到菲波纳奇比率的影子:
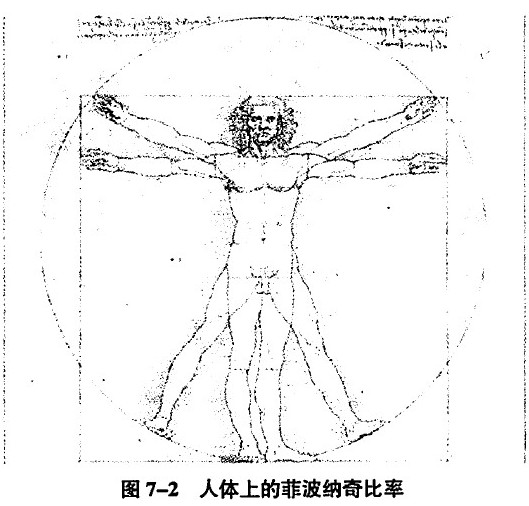
人的高度×肚脐到地面的高度=1.618(请看图7-2)
肩膀到指尖的距离×肘关节到指尖的距离=1.618
臀部到地面的距离×膝盖到地面的距离=1.618
蜂巢里雄蜂:雌蜂=1.618

2000多年前,古希腊雅典学派的第三大算学家欧道克萨斯首先提出了黄金分割。所谓黄金分制,指的是把长为L的线段分为两部分,使其中一部分对于全部之比等于另一部分对于该部分之比。黄金分割在文艺复兴前后经过阿拉伯人传入欧洲,受到了欧洲人的欢迎,他们称之为“金法”,17世纪欧洲的一位数学家甚至称它为“各种算法中最可宝贵的算法”。这种算法在印度被称为“三率法”或“三数法则”,也就是我们现在常说的比例方法。
其实有关“黄金分割”,我国也有记载。虽然没有古希腊早,但它是我国古代数学家独立创造的,后来传入了印度。经考证,欧洲的比例算法是源于我国,经过印度由阿拉伯传入欧洲的,而不是直接从古希腊传人的。
因为它在造型艺术中具有美学价值,在工艺美术和日用品的长宽设计中,采用这一比值能够引起人们的美感,其在实际生活中的应用也非常广泛,建筑物中某些线段的比就科学地采用了黄金分割,舞台上的报幕员并不是站在舞台的正中央,而是偏在台上一侧,以站在舞台长度的黄金分割点的位置最美观,声音传播得最好。就连植物界也有采用黄金分割的地方,如果从一棵嫩枝的顶端向下看,就会看到叶子是按照黄金分割的规律排列着的。在很多科学实验中,选取方案常用一种0.618法,即优选法,它可以使我们合理地安排较少的试验次数找到合理的和合适的工艺条件。正因为它在建筑、文艺、工农业生产和科学实验中有着广泛而重要的应用,所以人们才珍贵地称它为“黄金分割”。
1.菲波纳奇数列与交易
让我们首先从一个数列开始,它的前面几个数是1,1,2,3,5,8,13,21,34,55,89,144……这个数列的名字叫做“菲波纳奇数列”,这些数被称为“菲波纳奇数字”。其特点是除前两个数(数值为1)之外,每个数都是它前面两个数之和。
菲波纳奇数列与黄金分割有什么关系呢?经研究发现,相邻两个菲波纳奇数的比值是随序号的增加而逐渐趋于黄金分割比的,即f(n)/f(n-1)→0.618……由于菲波纳奇数都是整数,两个整数相除之商是有理数,所以只是逐渐逼近黄金分割比这个无理数。但是当我们继续计算出后面更大的菲波纳奇数时,就会发现相邻两数之比确实是非常接近黄金分割比的。
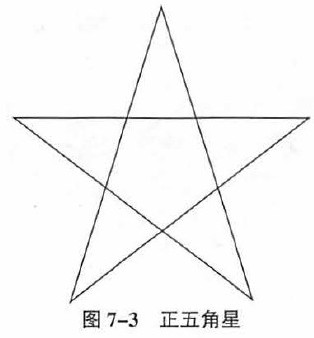
一个很能说明问题的例子是五角星(请看图7-3)。五角星是非常美丽的,这是为什么?因为在五角星中可以找到的所有线段之间的长度关系都是符合黄金分割比的。正五边形对角线连满后出现的所有三角形,都是黄金分割三角形。
菲波纳奇比率怎么会与交易扯上关系呢?外汇市场是一个群体行为发生的场所,同时也是整个宇窗的一部分,菲波纳奇比率是整个宇宙秩序的一个部分,在宇宙中的任何事物中得到体现,所以菲波纳奇比率必然以各种或隐或现的方式体现在金融产品的价格走势中,无论是股票市场,还是黄金市场都是如此。菲被纳奇比率主要体现在金融市场走势的时间和空间两个维度,但以空间维度的运用最多。在菲波纳奇比率的空间维度运用中,波段和波段之间的价格幅度是最主要的研判对象,本课的第二节对这方面的问题进行了一定程度的介绍。



