从概率角度考虑问题
很多人都在高中或大学里学过概率和统计学课程。毫无疑问,你可能看过像图4-1这样的分布图。
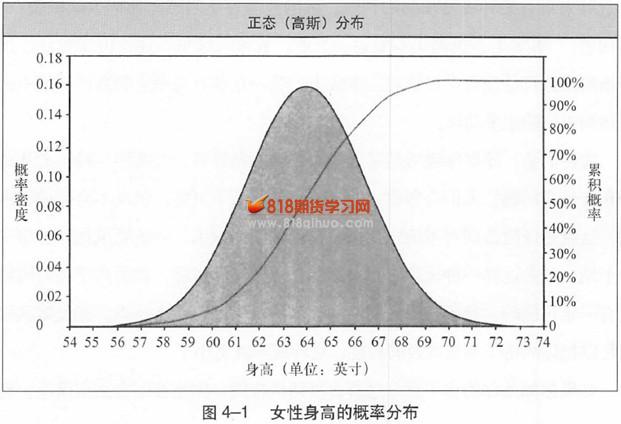
图4-1就是一个所谓的正态分布图。这个图反映了女性身高的分布状况。横轴是以英寸为单位的身高值,左右两个纵轴分别代表以下两种概率:
1.概率密度:阴影区域与左侧的刻度相对,它表示特定身高值所对应的概率。根据这张图,女性的平均身高是64英寸(约合1.63米)。一个女性的身高接近这个平均值的概率较大,离这个平均值越远,概率越小。图中央的最高点就是最大的概率,两侧较低的区域代表较小的概率。比如,70英寸(约合1.78米)处的曲线高度比68英寸(约合1.73米)处低很多,这说明一个女性身高达到70英寸的概率比达到68英寸的概率小得多。
2.累积概率:图中的实线与右侧的刻度相对,从零一直延伸到100%。它表示一个女性的身高不高于某个水平的概率。比如,这条实线在70英寸左右的身高水平上升到了几乎100%的程度。确切数值是99.18%,这意味着只有不到1%的女性能达到70英寸以上的高度。
这张图和其他类似的分布图都是用复杂的数学公式得出的,但它们都代表着一个简单的概念:距离代表平均水平的中心点越远,概率就越低。
但我们何必把概率问题搞得这么复杂呢。就算你不去理会那些数学知识和公式,你也一样可以用简单的方法做出像图4-1这样的图:首先,找一个女性比较多的地方,比如说大学校园;接下来,随机选择100位女性,测量一下她们的身高;最后,把这些身高数据按1英寸的间隔分成若干档,然后算一下每一档中有多少人。如果这么做,你很可能发现身高为64英寸有人数是16,63英寸和65英寸大约各有15人,62英寸和66英寸差不多各有12人,61英寸和67英寸各有8人,60英寸和68英寸各有8人,59英寸和69英寸各有2人,58英寸和70英寸各有1人。
如果你根据每一个特定身高值所对应的人数做出一个条形图,这个图会是图4-2这样的:
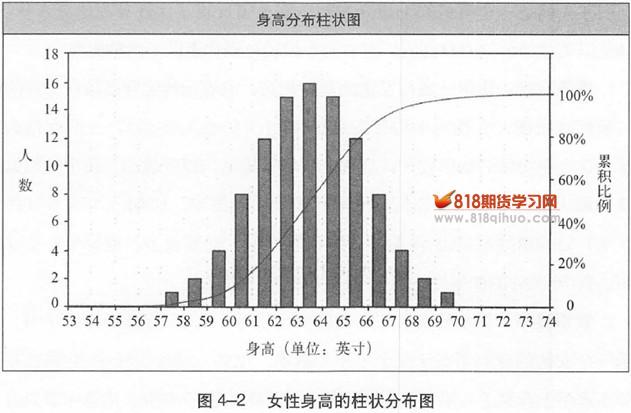
图4-2这样的图被称为柱状图。它反映了某个特定指标值和其他相近指标值的出现频率(在本例中,这个指标是女性的身高)。图4-2的形状与图4-1的正态分布图大同小异,但好处是你不用复杂的数学公式也可以做出这样的图,只要你会数数和归类就行了。
这一类柱状图也可以从你的交易系统中得出,让你对未来的走势有一个基本的概念;它可以帮助你从概率角度思考问题,而不是去预测些什么。图4-3就是这样一个柱状图,它是对一个简化版的海龟系统——唐奇安趋势系统的一次20年间月度回报率的测试结果。除了比海龟系统更简单外,这个系统的表现也优于海龟系统。
- 上一篇:避免预测未来
- 下一篇:对自己的交易结果负责



