最优化矛盾
还有一种效应会造成历史测试结果与实际交易结果的差异,我称之为最优化矛盾。这个矛盾制造了很多困惑,对刚刚接触电脑模拟技术的新人来说尤其如此。有些交易系统需要用特定的数值进行计算,选择这些数值的过程就是最优化。这些数值被称为参数。比如,长期移动均线的计算天数就是一个参数,短期均线的计算天数也是一个参数。最优化就是为这些参数选择最佳或最优化数值的过程。有许多交易者认为最优化不是件好事,因为它会导致曲线拟合现象和拙劣的表现。我说这是一派胡言!
如果操作得当,最优化是件好事,因为了解参数变化的影响总比忽略这种影响要好。当我们检验参数变化的效果时,我们常常能从一些迹象中发现系统的表现是随机效应或曲线拟合的结果,而不是系统优势的反映。所谓最优化过程,无非就是观察一下调整参数值对交易结果的影响,合理地决定在实际交易中使用什么样的参数值。
有些交易者之所以认为最优化有害或有危险性,只是因为他们不理解最优化矛盾,而且曾见识过不恰当最优化的恶果——这种不恰当的最优化正是统计学中所说的过度拟合现象的根源。
所谓最优化矛盾,是指参数最优化过程有两种相互矛盾的效果:一方面可以提高系统在未来表现良好的概率,另一方面却会降低系统的未来表现符合模拟测试结果的概率。这样,参数最优化虽然提高了系统的预期表现,但也降低了历史模拟指标的预测价值。我相信,正是因为对这种矛盾理解不足,许多交易者才会怀着对过度最优化和曲线拟合的恐惧而对最优化避之唯恐不及。但在我看来,恰当的最优化永远是明智的。
使用恰当的最优化所得出的参数值可以提高系统在实际交易中获得理想结果的可能性。一个例子有助于我们理解这一点。考虑一下布林格突破系统,它有两个参数:一个是长期均价,一个是标准差,一定时间内的长期均价加减一定倍数的标准差就是系统的波幅通道。图11-1反映了这个系统在不同标准差参数值下的MAR比率,横轴代表通道宽度,也就是标准差倍数,从1倍到4倍不等。
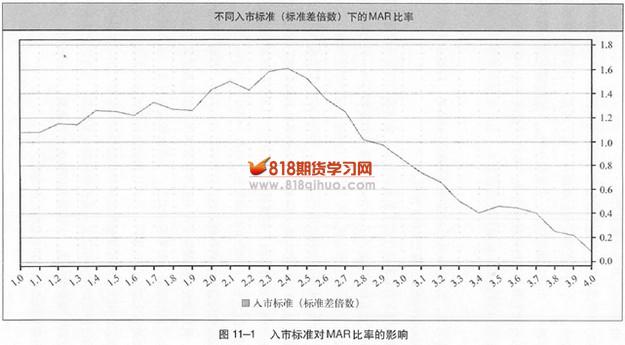
图中可见,2.4倍标准差对应着最好的模拟结果。任何小于或大于2.4倍标准差的入市标准都会降低MAR比率。
现在我们来看看最优化是不是真的有益。假设我们没有考虑通道宽度的最优化,而是凭主观感觉选择了一个3倍标准差的参数值——因为我们记得统计学课本说过,对正态分布来说,有99%以上的值会落到均值加减3倍标准差的范围内。如果未来与过去的差别不是太大,那我们会错失很多利润,而且我们的衰落幅度比2.4倍标准差要大得多。差距大到什么程度呢?看几个数据就知道了:在10年半的时间内,假设衰落水平相同,2.4倍标准差下的利润是3倍标准差的8倍之多,两者的年均回报率之比是54.5%比28.2%。
不做最优化意味着糊里糊涂地被运气因素完全左右。发现了调整这个参数的影响,我们就更好地理解了入市标准参数的作用和交易结果对这个参数的敏感性。现在我们知道,如果通道太窄,交易次数就会过多,这会削弱系统的表现自如果通道太宽,你在等待入市的过程中会白白错过很多趋势,这也对系统不利。如果你因为害怕过度最优化和曲线拟合而放弃最优化,你就得不到这种认识,而这种认识本来可以大大地改善你的交易结果,也为你在未来设计更好的系统提供一些新的理念。下面将介绍其他几个参数,你会看到,它们的变动同样对应着系统表现的山峰或山丘形变化。
移动均线参数
图11-2反映了移动平均收盘价的计算天数对MAR比率的影响,移动均价的计算天数能决定布林线披幅通道的中心线,从150天到500天不等。
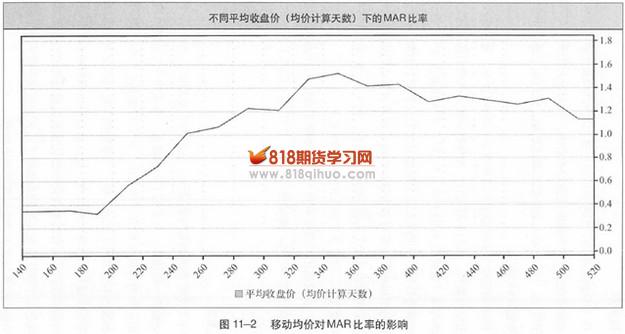
如图所示,350日对应着最佳的测试结果。任何大于或小于350日的参数值都会降低MAR比率。



